name: inverse layout: true class: center, middle, inverse --- # Geospatial Coordinate Encoder Chetan Surpur, Numenta .footnote[(Implemented in NuPIC)] --- layout: false # What's an Encoder? An encoder takes raw sensory input, and outputs a binary array of neuron activations. ##### Property: Semantically similar inputs should have overlapping bits in the outputs. 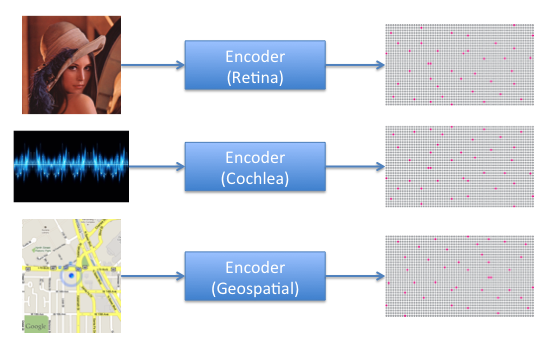 --- # Encoder Properties Imagine you're trying to encode a series of GPS coordinates. What properties should the encoded representations have? 1. Positions spatially close together should have overlapping bits in the encoding. 2. When moving at low speeds, resolution of movement should be more fine, and when moving at high speeds, resolution of movement should be more coarse (see next slide). --- ## Resolution property  --- class: center, middle # Geospatial Coordinate Encoder --- ## Initialize 1. Divide up the space into a grid of little squares. 2. Assign each square a random value between 0 and 1 (this is the square's `order`). 3. Map each square randomly to one of the bits in the output. --- ## Initialize (continued)  --- ## Initialize (continued) - The size of the square is a parameter to the encoder (called `scale`). - The `order` is a way to deterministically order the squares relative to each other (used later). - We can use a deterministic uniform hash function to generate the square `order` and corresponding output bit. That way, we can generate these values as-needed, and support an infinite space. --- ## Encode Given an input (GPS reading: `latitude`, `longitude`, `speed`), produce an output (binary vector). 1. Find the square in the grid that this GPS coordinate falls in (using a map projection*). 2. Draw a box around the square, with a certain radius. 3. Choose the top `W` squares (by `order`) that are contained in this box. 4. Activate the chosen squares' corresponding bits in the output. .footnote[*Currently, we're using the same map projection as Google Maps (the Spherical Mercator projection).] --- ## Encode (continued)  --- ## Encode (continued) ### Square size Note that every position that falls in a particular square will have an identical representation. Thus, the size of the squares indicates the maximum resolution of the encoder. The size of the squares is a parameter to the encoder called `scale`. The smaller this parameter, the higher the maximum resolution of the encoder, and the longer it takes to generate an encoding (since it has to look at more squares per encoding). --- ## Encode (continued) ### Properties Notice that this satisfies Property #1*. Positions close together will have overlapping boxes, so they'll likely share the highest-order squares. But what about Property #2⁺? .footnote[ * 1. Positions spatially close together should have overlapping bits in the encoding. ⁺ 2. When moving at low speeds, resolution of movement should be more fine, and when moving at high speeds, resolution of movement should be more coarse. ] --- ## Encode (modified) Given an input (GPS reading: `latitude`, `longitude`, `speed`), produce an output (binary vector). 1. Find the square in the grid that this GPS coordinate falls in (using a map projection). 2. Draw a box around the square, .red[with a radius proportional to `speed`]. 3. Choose the top `W` squares (by `order`) that are contained in this box. 4. Activate the chosen squares' corresponding bits in the output. --- ## Encode (modified) (continued) .pull-left[  ] .pull-right[  ] Now, the same distance traversed when moving at a higher speed translates to more overlap in the boxes, so more bits will overlap in the output. This satisfies Property #2. --- # Demo  --- class: center, middle # Coordinate Encoder --- # Coordinate Encoder The Coordinate Encoder is a generalization of the above ideas. Instead of (latitude, longitude, speed), it takes (coordinates, radius). `coordinates` determines the position to be encoded, and can be in any number of dimensions. `radius` determines the radius of the box drawn around the position. .footnote[Note: the Geospatial Coordinate Encoder is implemented as a subclass of the Coordinate Encoder.] --- # Advantages - Can be used to encode a position in an infinite space of any number of dimensions. - Runs in `O(N)` time where `N` is the number of squares contained in the box. - Special case: When `# of dimensions = 1`, it becomes a scalar encoder. Set the radius based on the past statistics of the data, and you have a scalar encoder with dynamic resolution! --- class: center, middle # Resources --- ### Geospatial Coordinate Encoder https://github.com/numenta/nupic/blob/master/nupic/encoders/geospatial_coordinate.py ### Coordinate Encoder https://github.com/numenta/nupic/blob/master/nupic/encoders/coordinate.py ### Geospatial Anomaly Demo using the encoder https://github.com/numenta/nupic.geospatial  --- class: center, middle, inverse # Thank you. ## Questions? .footnote[csurpur@numenta.org]